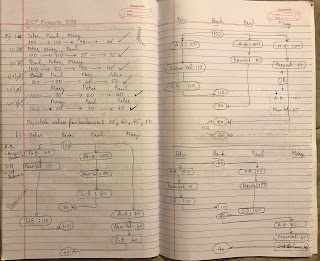
SICP Exercise 3.40 parallel-execute
Exercise 3.40. Give all possible values of x that can result from executing (define x 10) (parallel-execute (lambda () (set! x (* x x))) (lambda () (set! x (* x x x)))) Which of these possibilities remain if we instead use serialized procedures: (define x 10) (define s (make-serializer)) (parallel-execute (s (lambda () (set! x (* x x)))) (s (lambda () (set! x (* x x x))))) SOLUTION When there is no serialization: 1000000: P1 executes fully first, then P2 executes 1000000: P2 executes fully first, then P1 executes 10000: P2 changes x from 10 to 1000 between th...