SICP Exercise 3.25 make-table generalized

Exercise 3.25.  Generalizing one- and two-dimensional tables, show how to implement a table in which values are stored under an arbitrary number of keys and different values may be stored under different numbers of keys. The lookup and insert! procedures should take as input a list of keys used to access the table.

 SOLUTION

 The code is here.

 The table structure can be seen here.
Supported table structure is something like:

TABLE
--------
K1: val1
K2: val2
K3: val3
K31: val31
K32: (no value)
K321: val321
K322: val322
K33: val33
K4: val4

So the key combinations to retrieve data would be:

K1 retrieves val1
K2 retrieves val2
K3 retrieves val3
K3, K31 retrieves val31
K3, K32, K321 retrieves val321
K3, K32, K322 retrieves val322
K3, K33 retrieves val33
K4 retrieves val4

Note: I want to allow for the possibility for not just primitives like string literals and numbers but objects to be inserted and looked up from the table. Since every non-primitive object is implemented using pairs, this makes it necessary for us to be able to distinguish between a sub-table and a value which is an object. So I am introducing tags so that the table procedures can correctly identify the data they handle as they traverse through the table. So a 'key' will not be just a string literal but a pair in which the 'car' is a tag with the value 'key and the 'cdr' is the actual key. Similarly, a 'value' will not just be a string literal but a pair in which the 'car' is a tag with the value 'value and the 'cdr' is the actual value which could be a primitive or a complex object.

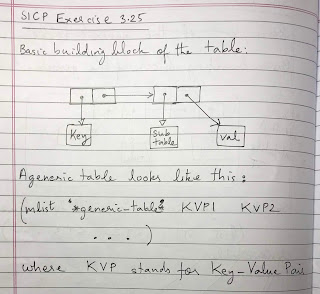
The basic building block of this table is a key-value pair. It is a pair in which the 'car' is the key and the 'cdr' is another pair in which the 'car' is a pointer to a generic table and the 'cdr' is the value. This structure allows us to create an arbitrary number of levels in the table. If it is just a simple key-value pair with no sub-keys, then the contained generic table will be null. If it is a key with sub-keys but no value for this key, then the contained generic table will be non-null and the value will be null. And of course, both the contained generic table and the value can be non-null to allow for data like:

K3, K31: val31
K3, K32, K321: val321

 And the structure of this generic table with an arbitrary
number of levels is:

 (mlist '*generic-table* KVP1 KVP2 ....)

 where KVP stands for key-value pair.

The logic for inserting a key list and its associated value:

Look for the first key from the key-list in the first level of the table. If found, then look for the 2nd key in the sub-table pointed to by the first key and continue this process. If all the keys are found, then the insert operation will replace the existing value with the new value. If at any level the key is not found, then insert that key at that level in the table and continue inserting keys below it and finally the value.

As with the other exercises, I have implemented a print-table procedure for printing the entire table (with indentations that signify the level of the key) in an easy-to-read manner.

 See this diagram:

Comments

Post a Comment

Popular posts from this blog

SICP Exercise 2.56 differentiation rule

Image
Exercise 2.56.    Show how to extend the basic differentiator to handle more kinds of expressions. For instance, implement the differentiation rule by adding a new clause to the  deriv  program and defining appropriate procedures  exponentiation? ,  base ,  exponent , and  make-exponentiation . (You may use the symbol  **  to denote exponentiation.) Build in the rules that anything raised to the power 0 is 1 and anything raised to the power 1 is the thing itself. SOLUTION The code and tests are here .
Read more

SICP Exercise 1.28 (Miller-Rabin Test)

Exercise 1.28.    One variant of the Fermat test that cannot be fooled is called the  Miller-Rabin test  (Miller 1976; Rabin 1980). This starts from  an alternate form of Fermat's Little Theorem, which states that if  n  is a prime number and  a  is any positive integer less than  n , then  a  raised to the ( n  - 1)st power is congruent to 1 modulo  n . To test the primality of a number  n  by the Miller-Rabin test, we pick a random number  a < n  and raise  a  to the ( n  - 1)st power modulo  n  using the  expmod  procedure. However, whenever we perform the squaring step in  expmod , we check to see if we have discovered a ``nontrivial square root of 1 modulo  n ,'' that is, a number not equal to 1 or  n  - 1 whose square is equal to 1 modulo  n . It is possible to prove that if such a nontrivial square root of 1 exists, then  n  is not prime. It is also possible to prove that if  n  is an odd number that is not prime, then, for at least half the numbers a < n , co
Read more

SICP Exercise 4.18 a alternative strategy for interpreting internal definitions

Exercise 4.18.   Consider an alternative strategy for scanning out definitions that translates the example in the text to (lambda < vars >   (let ((u '*unassigned*)         (v '*unassigned*))     (let ((a < e1 >)           (b < e2 >))       (set! u a)       (set! v b))     < e3 >)) Here  a  and  b  are meant to represent new variable names, created by the interpreter, that do not appear in the user's program. Consider the  solve  procedure from section  3.5.4 : (define (solve f y0 dt)   (define y (integral (delay dy) y0 dt))   (define dy (stream-map f y))   y) Will this procedure work if internal definitions are scanned out as shown in this exercise? What if they are scanned out as shown in the text? Explain. SOLUTION & DISCUSSION The streams based procedure 'solve' in this exercise exposed several issues in my metacircular evaluator implementation. I discovered that streams are not at all handled properly by my evaluator. Moreover, the &
Read more