SICP

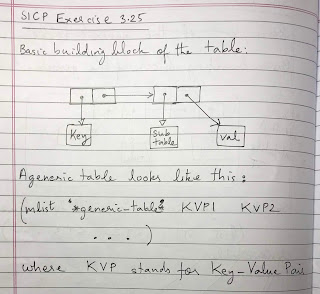
Exercise 3.25.    Generalizing one- and two-dimensional tables, show how to implement a table in which values are stored under an arbitrary number of keys and different values may be stored under different numbers of keys. The  lookup  and  insert!  procedures should take as input a list of keys used to access the table. SOLUTION The code is here . The table structure can be seen here . Supported table structure is something like: TABLE -------- K1: val1 K2: val2 K3: val3 K31: val31 K32: (no value) K321: val321 K322: val322 K33: val33 K4: val4 So the key combinations to retrieve data would be: K1 retrieves val1 K2 retrieves val2 K3 retrieves val3 K3, K31 retrieves val31 K3, K32, K321 retrieves val321 K3, K32, K322 retrieves val322 K3, K33 retrieves val33 K4 retrieves val4 Note: I want to allow for the possibility for not just primitives like string literals and numbers  but obj...

Exercise 3.24.    In the table implementations above, the keys are tested for equality using  equal?  (called by  assoc ). This is not always the appropriate test. For instance, we might have a table with numeric keys in which we don't need an exact match to the number we're looking up, but only a number within some tolerance of it. Design a table constructor  make-table  that takes as an argument a  same-key?  procedure that will be used to test ``equality'' of keys.  Make-table  should return a  dispatch  procedure that can be used to access appropriate  lookup  and  insert!  procedures for a local table. SOLUTION The code is here . Aside from supporting same-key?, I have also implemented a 'print-table' procedure. I expect this to be useful in later exercises too.

Exercise 3.23.    A  deque  (``double-ended queue'') is a sequence in which items can be inserted and deleted at either the front or the rear. Operations on deques are the constructor  make-deque , the predicate  empty-deque? , selectors  front-deque  and  rear-deque , and mutators  front-insert-deque! ,  rear-insert-deque! ,  front-delete-deque! , and  rear-delete-deque! . Show how to represent deques using pairs, and give implementations of the operations.   All operations should be accomplished in theta (1) steps. SOLUTION The code is here . The diagram here explains the design:

Exercise 3.22.    Instead of representing a queue as a pair of pointers, we can build a queue as a procedure with local state. The local state will consist of pointers to the beginning and the end of an ordinary list. Thus, the  make-queue  procedure will have the form (define (make-queue)   (let ((front-ptr  ... )         (rear-ptr  ... ))     < definitions of internal procedures >     (define (dispatch m)  ... )     dispatch)) Complete the definition of  make-queue  and provide implementations of the queue operations using this representation. SOLUTION The code is here: SICP Exercise 3.22 make-queue as procedure with local state

Exercise 3.21.   Ben Bitdiddle decides to test the queue implementation described above. He types in the procedures to the Lisp interpreter and proceeds to try them out: (define q1 (make-queue)) (insert-queue! q1 'a) ((a) a) (insert-queue! q1 'b) ((a b) b) (delete-queue! q1) ((b) b) (delete-queue! q1) (() b) ``It's all wrong!'' he complains. ``The interpreter's response shows that the last item is inserted into the queue twice. And when I delete both items, the second  b  is still there, so the queue isn't empty, even though it's supposed to be.'' Eva Lu Ator suggests that Ben has misunderstood what is happening. ``It's not that the items are going into the queue twice,'' she explains. ``It's just that the standard Lisp printer doesn't know how to make sense of the queue representation. If you want to see the queue printed correctly, you'll have to define your own print procedure for queues.'' Expl...

Exercise 3.20.   Draw environment diagrams to illustrate the evaluation of the sequence of expressions (define x (cons 1 2)) (define z (cons x x)) (set-car! (cdr z) 17) (car x) 17 using the procedural implementation of pairs given above. (Compare exercise  3.11 .) Solution: The attached pictures show the progression of the environment structure as the sequence of interactions happens as specified in this exercise. The github links are: Page 1 Page 2 Page 3 Page 4 Page 5 The slides to the same diagrams are  here

Exercise 3.19.   Redo exercise  3.18  using an algorithm that takes only a constant amount of space. (This requires a very clever idea.) SOLUTION I use the definition of an iterative process from section 1.2.1. here. Scheme will execute an iterative process in constant space, even if the iterative process is  described by a recursive procedure. An implementation with this property is called  tail-recursive. With a tail-recursive implementation, iteration can be expressed using the  ordinary procedure call mechanism.  In general, an iterative process is one whose state can be summarized by a fixed number of  state variables, together with a fixed rule that describes how the state variables should be  updated as the process moves from state to state and an (optional) end test that specifies  conditions under which the process should terminate. The program variables provide a complete  description of the state of the...

Exercise 3.18.    Write a procedure that examines a list and determines whether it contains a cycle, that is, whether a program that tried to find the end of the list by taking successive  cdr s would go into an infinite loop. Exercise  3.13  constructed such lists. SOLUTION This program expects an ordinary linked list as in exercise 3.13. If given a  more complex structure with multiple cycles, it will miss detecting cycles that don't  lie on the 'main' path. The 'main' path is the path traversed by successive cdrs from the  root pair. I deliberately kept it simple.  I reasoned that if we want to write a more generic cycle detector that can find all  cycles in a complex structure, then this program can be used as a component there. This  will allow us to keep modularity in our design. The code is here: Exercise 3.18 detect cycle