SICP Exercise 1.23 (Skip Even Divisors)

Exercise 1.23.  The smallest-divisor procedure shown at the start of this section does lots of needless testing: After it checks to see if the number is divisible by 2 there is no point in checking to see if it is divisible by any larger even numbers. This suggests that the values used for test-divisor should not be 2, 3, 4, 5, 6, ..., but rather 2, 3, 5, 7, 9, .... To implement this change, define a procedure next that returns 3 if its input is equal to 2 and otherwise returns its input plus 2. Modify the smallest-divisor procedure to use (next test-divisor) instead of (+ test-divisor 1). With timed-prime-test incorporating this modified version of smallest-divisor, run the test for each of the 12 primes found in exercise 1.22. Since this modification halves the number of test steps, you should expect it to run about twice as fast. Is this expectation confirmed? If not, what is the observed ratio of the speeds of the two algorithms, and how do you explain the fact that it is different from 2?

 SOLUTION

 The code and tests are here.

Observations
============

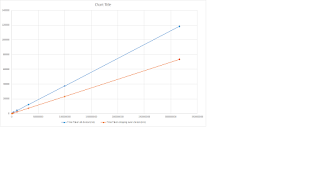
 Generally takes lesser time than when we don't skip even numbers while testing
divisors. But, the number is not near half of the previous number (as we might expect)

 Observed Ratios
===============

 Observed ratios keep dropping as the numbers get larger and stabilize near
1.5. (For large numbers, the fluctuations caused by other processes in the
computer become less significant.) The reason it is not 2 is that there is an
extra conditional being checked inside the 'next' procedure.



Comments

Post a Comment

Popular posts from this blog

SICP Exercise 2.56 differentiation rule

Image
Exercise 2.56.    Show how to extend the basic differentiator to handle more kinds of expressions. For instance, implement the differentiation rule by adding a new clause to the  deriv  program and defining appropriate procedures  exponentiation? ,  base ,  exponent , and  make-exponentiation . (You may use the symbol  **  to denote exponentiation.) Build in the rules that anything raised to the power 0 is 1 and anything raised to the power 1 is the thing itself. SOLUTION The code and tests are here .
Read more

SICP Exercise 1.28 (Miller-Rabin Test)

Exercise 1.28.    One variant of the Fermat test that cannot be fooled is called the  Miller-Rabin test  (Miller 1976; Rabin 1980). This starts from  an alternate form of Fermat's Little Theorem, which states that if  n  is a prime number and  a  is any positive integer less than  n , then  a  raised to the ( n  - 1)st power is congruent to 1 modulo  n . To test the primality of a number  n  by the Miller-Rabin test, we pick a random number  a < n  and raise  a  to the ( n  - 1)st power modulo  n  using the  expmod  procedure. However, whenever we perform the squaring step in  expmod , we check to see if we have discovered a ``nontrivial square root of 1 modulo  n ,'' that is, a number not equal to 1 or  n  - 1 whose square is equal to 1 modulo  n . It is possible to prove that if such a nontrivial square root of 1 exists, then  n  is not prime. It is also possible to prove that if  n  is an odd number that is not prime, then, for at least half the numbers a < n , co
Read more

SICP Exercise 4.18 a alternative strategy for interpreting internal definitions

Exercise 4.18.   Consider an alternative strategy for scanning out definitions that translates the example in the text to (lambda < vars >   (let ((u '*unassigned*)         (v '*unassigned*))     (let ((a < e1 >)           (b < e2 >))       (set! u a)       (set! v b))     < e3 >)) Here  a  and  b  are meant to represent new variable names, created by the interpreter, that do not appear in the user's program. Consider the  solve  procedure from section  3.5.4 : (define (solve f y0 dt)   (define y (integral (delay dy) y0 dt))   (define dy (stream-map f y))   y) Will this procedure work if internal definitions are scanned out as shown in this exercise? What if they are scanned out as shown in the text? Explain. SOLUTION & DISCUSSION The streams based procedure 'solve' in this exercise exposed several issues in my metacircular evaluator implementation. I discovered that streams are not at all handled properly by my evaluator. Moreover, the &
Read more