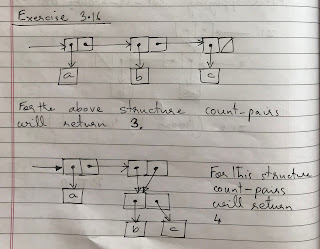
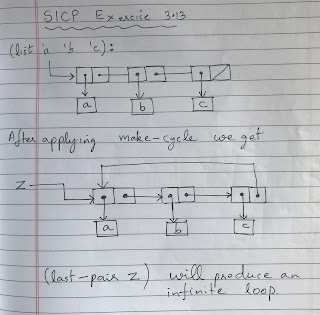
SICP Exercise 3.17 correct count-pairs

Exercise 3.17. Devise a correct version of the count-pairs procedure of exercise 3.16 that returns the number of distinct pairs in any structure. (Hint: Traverse the structure, maintaining an auxiliary data structure that is used to keep track of which pairs have already been counted.) SOLUTION The code is here: Exercise 3.17 correct count-pairs The explanation and the box-and-pointer diagram is here: Diagram