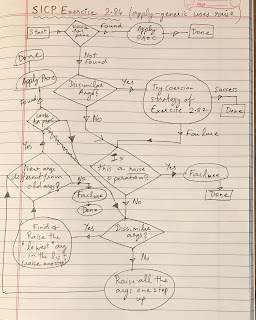
SICP Exercise 2.91 polynomial long division
Exercise 2.91. A univariate polynomial can be divided by another one to produce a polynomial quotient and a polynomial remainder. For example, Division can be performed via long division. That is, divide the highest-order term of the dividend by the highest-order term of the divisor. The result is the first term of the quotient. Next, multiply the result by the divisor, subtract that from the dividend, and produce the rest of the answer by recursively dividing the difference by the divisor. Stop when the order of the divisor exceeds the order of the dividend and declare the dividend to be the remainder. Also, if the dividend ever becomes zero, return zero as both quotient and remainder. We can design a div-poly procedure on the model of add-poly and mul-poly . The procedure checks to see if the two polys have the same variable. If so, div-poly strips off the variable and passes the problem to div-terms , which performs...