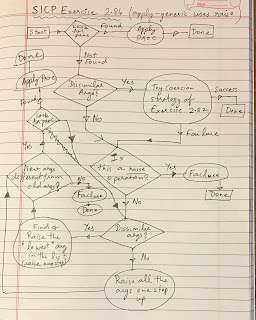
SICP Exercise 2.86 complex numbers with abstract parts
Exercise 2.86. Suppose we want to handle complex numbers whose real parts, imaginary parts, magnitudes, and angles can be either ordinary numbers, rational numbers, or other numbers we might wish to add to the system. Describe and implement the changes to the system needed to accommodate this. You will have to define operations such as sine and cosine that are generic over ordinary numbers and rational numbers. SOLUTION The code and tests are here . Here I have changed the generic procedures (real-part) and (imag-part) to (REAL-PART) and (IMAG-PART) in order to avoid name-conflicts with the Racket primitives (real-part) and (imag-part). I am using these primitives to understand more about Racket numbers.