SICP

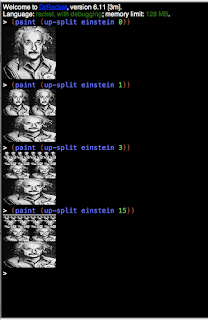
Exercise 2.45.    Right-split  and  up-split  can be expressed as instances of a general splitting operation. Define a procedure  split  with the property that evaluating (define right-split (split beside below)) (define up-split (split below beside)) produces procedures   right-split   and   up-split   with the same behaviors as the ones already defined. SOLUTION The code and tests are here . ; Test Results in the image(s) below

Exercise 2.44.   Define the procedure  up-split  used by  corner-split . It is similar to  right-split , except that it switches the roles of  below  and  beside . SOLUTON The code and tests are here . Test Results in the image below

Exercise 2.43.   Louis Reasoner is having a terrible time doing exercise  2.42 . His  queens  procedure seems to work, but it runs extremely slowly. (Louis never does manage to wait long enough for it to solve even the 6× 6 case.) When Louis asks Eva Lu Ator for help, she points out that he has interchanged the order of the nested mappings in the  flatmap , writing it as (flatmap  (lambda (new-row)    (map (lambda (rest-of-queens)           (adjoin-position new-row k rest-of-queens))         (queen-cols (- k 1))))  (enumerate-interval 1 board-size)) Explain why this interchange makes the program run slowly. Estimate how long it will take Louis's program to solve the eight-queens puzzle, assuming that the program in exercise  2.42  solves the puzzle in time  T . SOLUTIO...

Exercise 2.42.    Figure 2.8:   A solution to the eight-queens puzzle. The  ``eight-queens puzzle'' asks how to place eight queens on a chessboard so that no queen is in check from any other (i.e., no two queens are in the same row, column, or diagonal). One possible solution is shown in figure  2.8 . One way to solve the puzzle is to work across the board, placing a queen in each column. Once we have placed  k  - 1 queens, we must place the  k th queen in a position where it does not check any of the queens already on the board. We can formulate this approach recursively: Assume that we have already generated the sequence of all possible ways to place  k  - 1 queens in the first  k  - 1 columns of the board. For each of these ways, generate an extended set of positions by placing a queen in each row of the  k th column. Now filter these, keeping only the positions for which the queen in the  k th co...

Exercise 2.41.   Write a procedure to find all ordered triples of distinct positive integers  i ,  j , and  k  less than or equal to a given integer  n  that sum to a given integer  s . SOLUTION The code and tests are here .

Exercise 2.40.   Define a procedure  unique-pairs  that, given an integer  n , generates the sequence of pairs ( i , j ) with 1 <   j <  i <   n . Use  unique-pairs  to simplify the definition of  prime-sum-pairs  given above. SOLUTION The code and tests are here .